Full Prolog, Syntax and Semantics

1 Preface: Recursion in Prolog

We have already seen a recursive definition of live:

live(outside).
live(X) :- connected_to(X, Y), live(Y).

This has a base case: live(outside) is simply true.

It also has a recursive case: live(X) is true for any X if we can find any Y such that connected_to(X, Y) is true and live(Y) is true.

Prolog can now prove that some circuit element like p2 is live by repeatedly using the rule for live(X) until we reach outside and can refer to the base case.

1.1 Practical Recursion in Prolog

Why did we write

live(X) :- connected_to(X, Y), live(Y).

rather than

live(X) :- live(Y), connected_to(X, Y).

Logically, they both mean the same thing because the order of atoms in the body does not matter. (“And” is commutative and associative.) Prolog, however, always tries to establish the first goal first.

What will happen in Prolog if we try our second version of the live rule?

(Three Exercises.)

2 One Small Step to Full Prolog

In propositional logic an atom is a lowercase name (a predicate symbol).

Atoms can have arguments (terms) in Datalog like connected_to(w3, X). Each term can be a constant or variable, like w3 and X, respectively. (Prolog also allows several other simple types like numbers and strings.)

Full Prolog lets us use something that looks like an atom as a term. We call this a “function” or “compound term”. (I’ll prefer “compound term”, since function can get confusing!)

A compound term is a functor followed by a list of terms in parentheses like tree(7, empty_tree, tree(9, empty_tree, empty_tree)). Notice that a compound term can have any type of term as an argument, including more compound terms. Any predicate symbol can be used as a functor.

(Exercise.)

2.1 Our Own Version of Lists in Full Prolog

Why would we want this? Well, what if we want to represent lists? In Racket, we needed cons and empty to represent this. empty is no problem; it’s just a constant. cons, however, takes two arguments.

In Datalog, we could never have said something like length(cons(10, empty), 1). cons(10, empty) isn’t a term in Datalog.

In full Prolog, we can have terms like:

• cons(10, empty): a one-element list containing the number 10.
• cons(10, cons(20, empty)): a two-element list [10, 20]. Notice that a term can be a compound term, and the terms inside a compound term can be compound terms, recursively.

Now, we can create atoms like prefix(cons(10, empty), cons(10, cons(20, empty))). That might be a query that asks whether the list [10] is a prefix of the list [10, 20], which it is.

(Four exercises.)

Here are some files we’ll likely work on in class:

• my_length
• prefix
• dates and before

2.2 Syntactic “Sugar” for Lists

As in Haskell, Prolog gives us a simpler syntax for describing lists, but it’s really just a different way to write the same kind of thing we wrote above: compound terms.

• [] is the empty list
• [H|T] is like cons(H,T)
• [x, y, z] is a three-element list containing elements x, y, and z

We can even combine these as in: [x, y|Tail] is a list that starts with the first two elements x and y and then has Tail as the rest of the list.

Let’s rewrite prefix with this notation:

% prefix(List1, List2) is true if all the elements in
% List1 occur at the start of List2. This is our OLD version:
prefix(empty, _).
prefix(cons(X, Xs), cons(X, Ys)) :-
  prefix(Xs, Ys).

(Five Exercises.)

Let’s spend some time with these exercises investigating what these Prolog relations are (and are not) capable of!

Here are some files we’ll likely work on in class:

• prefix, again
• sublist

3 A Semantics for Individuals, Relations, and Terms

3.1 An “Interpretation” in Full Prolog

In propositional Prolog, our interpretations just gave truth values to simple atoms. Now, our atoms may be relations referring to constants (or numbers, strings, etc.), variables, or compound terms made up of more constants, variables, and terms.

Our semantics needs to handle these.

We start by assuming we have a variable assignment that maps each variable to a term.

If that term is a variable or is a compound term that contains variables, its variables can also be mapped to terms. We don’t allow this to go on forever: we have to be able to “walk” the variable out into a term containing no variables eventually, which we call a ground term.

Now that we’ve assumed that, we’ll set variables aside. We assume they have been “walked” away so that they are now ground terms.

Our interpretation specifies:

• what individuals (objects) are in the world
• the corresondence between symbols in the computer and elements of the world:
  • which individual each constant refers to
  • what function each compound term’s symbol refers to (a function from the individuals its terms refer to into the individual that the compound term itself refers to)
  • what relation each predicate symbol refers to

3.2 Formal Semantics

An interpretation I is a triple ⟨D, ϕ, π⟩, where:

• D, the domain, is a non-empty set. The elements of D are individuals.
• ϕ is a mapping that
  • assigns to each constant an individual: constant c denotes individual ϕ(c)
  • assigns to each compound term’s symbol an n-ary function f that maps from individuals for its n arguments to an individual for the whole compound term
• π is a mapping that assigns to each n-ary predicate symbol a relation, a function from Dⁿ (n individuals in the world) into T or F (true or false). If n = 0, then this is simply T or F, just like in our propositional semantics.

3.3 Example Interpretation

Imagine a desk with some items on it: a phone (📱), a pencil (✏️), and scissors (✂️).

We may have a Prolog program with:

• Constants: phone, pencil, telephone
• Predicate symbols: noisy/1, left_of/2

One interpretation of our program would be:

• D = {📱, ✏️, ✂️}
• ϕ(phone) = 📱, ϕ(pencil) = ✏️, ϕ(telephone) = 📱.
• π(noisy) is a function that maps: 📱 to T, ✏️ to F, and ✂️ to F.
• π(left_of) is a function f_l where:
  • f_l(📱,📱) = F, f_l(📱,✏️) = T, f_l(📱,✂️) = F
  • f_l(✏️,📱) = F, f_l(✏️,✏️) = F, f_l(✏️,✂️) = F
  • f_l(✂️,📱) = F, f_l(✂️,✏️) = T, f_l(✂️,✂️) = F

3.4 Points of Interest in an Interpretation

• The domain D can contain real things that cannot be stored in a computer (the concept of love, your friend, a course, a room).
• ϕ tells us which individual in D each constant represents, but:
  • two constants (like phone and telephone above) could represent the same thing
  • some individuals (like ✂️ above) may not be represented by a constant
• π(p) for some predicate p is itself a function. The function tells us when p is true and when it is false.

(Exercise.)

3.5 Truth in an Interpretation

Once we have an interpretation, we can tell whether any ground atom is true. The atom will be of the form p(t₁,…,t_n), where p is a predicate symbol, and each t_i is a term. To find out if p(t₁,…,t_n) is true:

1. Look up π(p). Call it f_p.
2. Get the individual o_i referred to by each term t_i.
   1. If t_i is a constant, then the individual is ϕ(t_i).
   2. Otherwise, t_i is a compound term like q(s₁,…,s_m).
      1. Recursively find each individual r_j associated with the terms s₁, …, s_m
      2. Get the function f_q = ϕ(q)
      3. Produce f_q(r₁,…,r_m): the individual the compound term refers to.
3. Now, p(t₁,…,t_n) is true exactly when f_p(o₁,…,o_n) is true.

In other words, we use the interpretation to recursively shift the pieces of the atom into their corresponding elements of the domain and then look up the truth value of the resulting relation.

Once we have the truth of atoms, the truth of conjunctions, rules, and knowledge bases works just like before. (A conjunction is true if both of its parts are true, a rule is true unless its body is true but its head is false, and a knowledge base is true if all of its clauses are true.)

Models still work the same way as well: a model of a KB is an interpretation that makes the KB true.

Logical consequence still works the same way: a goal g is a conjunction of atoms, and KB ⊨ g if g is true in every model of KB.

We still design our KB to encode our intended interpretation:

1. Choose a task domain as your intended intepretation
2. Associate constants with individuals you want to name (like animals or nodes in a script of steps you want to follow)
3. For each relation you want to represent, give it a predicate symbol in the program.
4. Axiomatize the domain by telling the system clauses that are true in the intended interpretation and describe it as fully as you need.
5. Ask questions about the intended interpretation using the symbols you’ve created.
6. Interpret the answers as meaningful in your intended interpretation.

The computer is still just manipulating meaningless symbols, but if we did a good job of encoding our intended interpretation and the system’s mechanical reasoning is sound, then we can interpret the answers as meaningful in our domain!

3.6 Another Example Interpretation

Here is a visualization of how we might consider the relationship between a program and a domain:

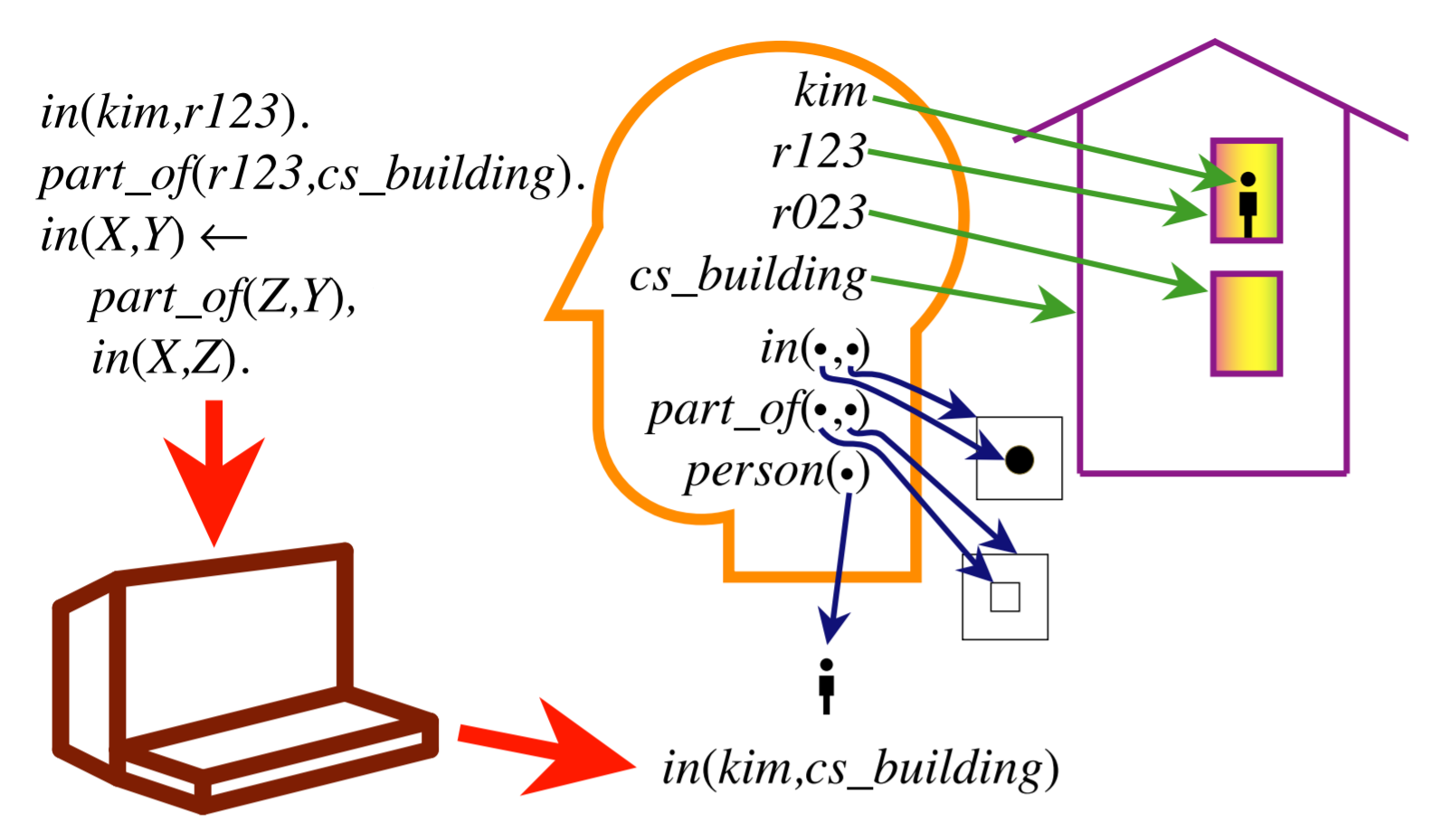
In the user’s mind, Kim is a person in a room in a building. The concept of being “in” something has specific meaning to the person, as does the concept of being “part of” something. They can tell when it’s true that one thing is in another or part of another. The user’s intended interpretation associates each element of the program with the individual or relationship they were considering in the domain.

If the KB is written well, then the intended interpretation is a model of the KB, and any logical consequence of the KB that Prolog derives is also true in the world. For example, Prolog can derive in(kim, cs_building), and we can interpret it to mean that Kim is in the CS building.

(Exercise.)

4 Tips on Writing Prolog Programs

To write a Prolog program:

1. Have a clear intended interpretation: what all predicates, functions and constants mean
2. Don’t tell lies.
   • Make sure all clauses are true given your meaning for the constants, functions, predicates.
   • Make sure that the clauses cover all of the cases when a predicate is true.
3. Avoid cycles. For example, be careful of predicates like path_between, which may end up with path_between(X, Y) :- path_between(Y, X).
4. To solve a complex problem break it into simpler problems.
   • Design top-down: Figure out the top-level predicates that you need. Write out their meanings and high-level notes on how they will work. Break them down in terms of simpler predicates.
   • Build bottom-up: Create, test, and debug the simplest predicates first. Then, build more complex ones on top of them.

For testing, you may want to use plunit. Here’s a plunit example.