Prolog as a Programming Language
Complete the associated in-class exercises.
1 A Procedural Model of Prolog Execution
We’ve related Prolog programs to logic and described how to view program execution as proof construction.
How is that implemented? We’ll understand this with the Prolog box model.
1.1 Debugging/Tracing Prolog Queries
Let’s try tracing a query on a small Prolog program:
:- dynamic f/0. % needed b/c f is otherwise undefined.
a :- b, c, d.
a :- e.
b.
c :- s.
c :- t.
d :- f.
e :- t.
e :- s.
s.
t.Run trace. Then ask: ?- a.1
(Any time you get a first answer, you can ask for more answers with semicolon ;. That’s true whether tracing or not.)
Prolog talks about call, exit, and redo. What does this mean?
1.2 Atoms as Procedures
We’ll imagine clauses defining the same atom as a procedure. (The clauses defining a single atom will be facts for that atom, or a set of rules with the atom as head. A procedure is an imperative “function”.)
- A procedure either succeeds or fails.
- To call a procedure, call each body in turn until one succeeds.
- To call a body, call each atom in the body.
- The procedure (and its body) succeeds if all atoms in the body succeed.
- The procedure fails if no bodies succeed.
Let’s visualize that and define our tracing terminology.
1.3 Call, Exit, Fail, and Retry (and Redo)
We’ll think of a Prolog atom/procedure as a box with four “ports” on it:
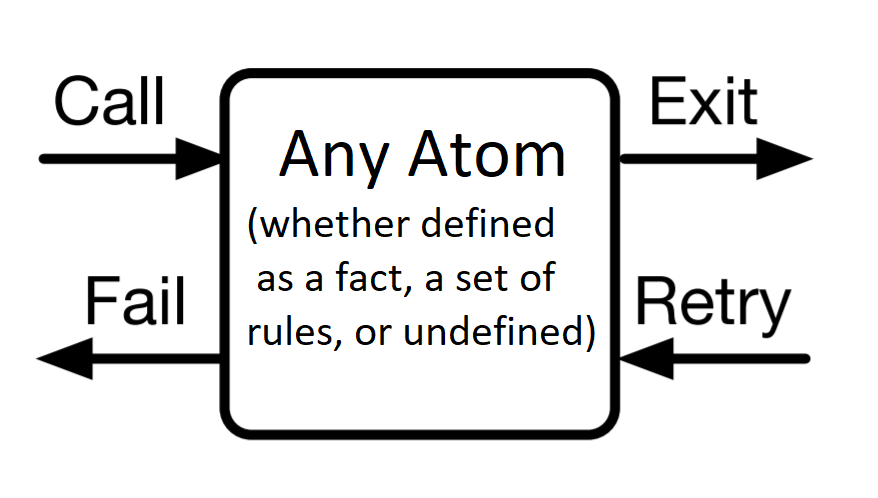
The ports are ways to “enter” the atom or “exit” it:
- We call into an atom when we want to establish it as part of our proof.
- We exit out of an atom when we have successfully established it (somehow).
- We fail out of an atom when we cannot establish it.
- We retry into an atom to seek an alternate way to establish it.2
SWI-Prolog’s tracing shows call and exit but uses “redo” to describing failing out of one rule’s body and calling into the next.
Aside: We can never fail an atom unless it was previously called (but lots can happen between the call and the fail). We can never retry an atom unless it previously exited (but lots can happen between the exit and the retry).
1.4 Boxes for Several Cases
We can now “wire up” our boxes to represent how particular clauses work.
How should we “wire up” a fact like a.? Any time we try to establish an atom with a fact, it automatically succeeds.
How should we “wire up” an undefined atom? Any time we try to etsablish an undefined atom, it automatically fails.
(Exercise.)
We can build up more complex cases by reasoning through Prolog’s mechanical proof model.
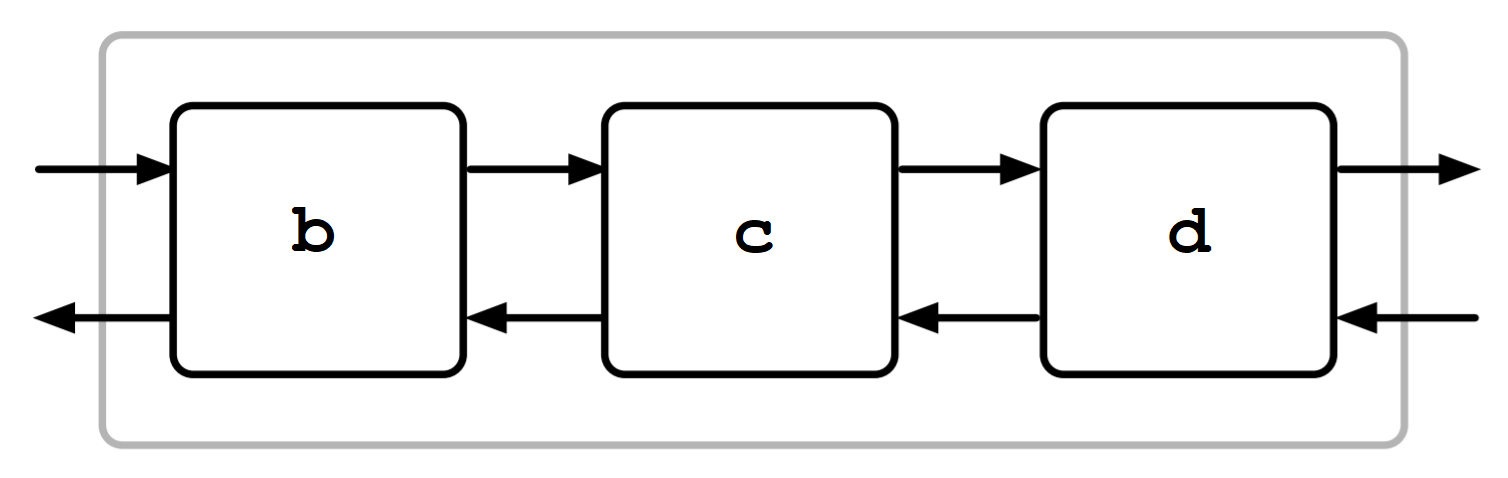
Consider an atom a defined only by the rule: a :- b, c, d. a succeeds when b and then c and then d succeeds. (Prolog imposes the order by always selecting the first subgoal first.)
Our box model for a looks like:
Consider an atom w defined only by the three rules:
w :- x.
w :- y.
w :- z.Our box model for w looks like:
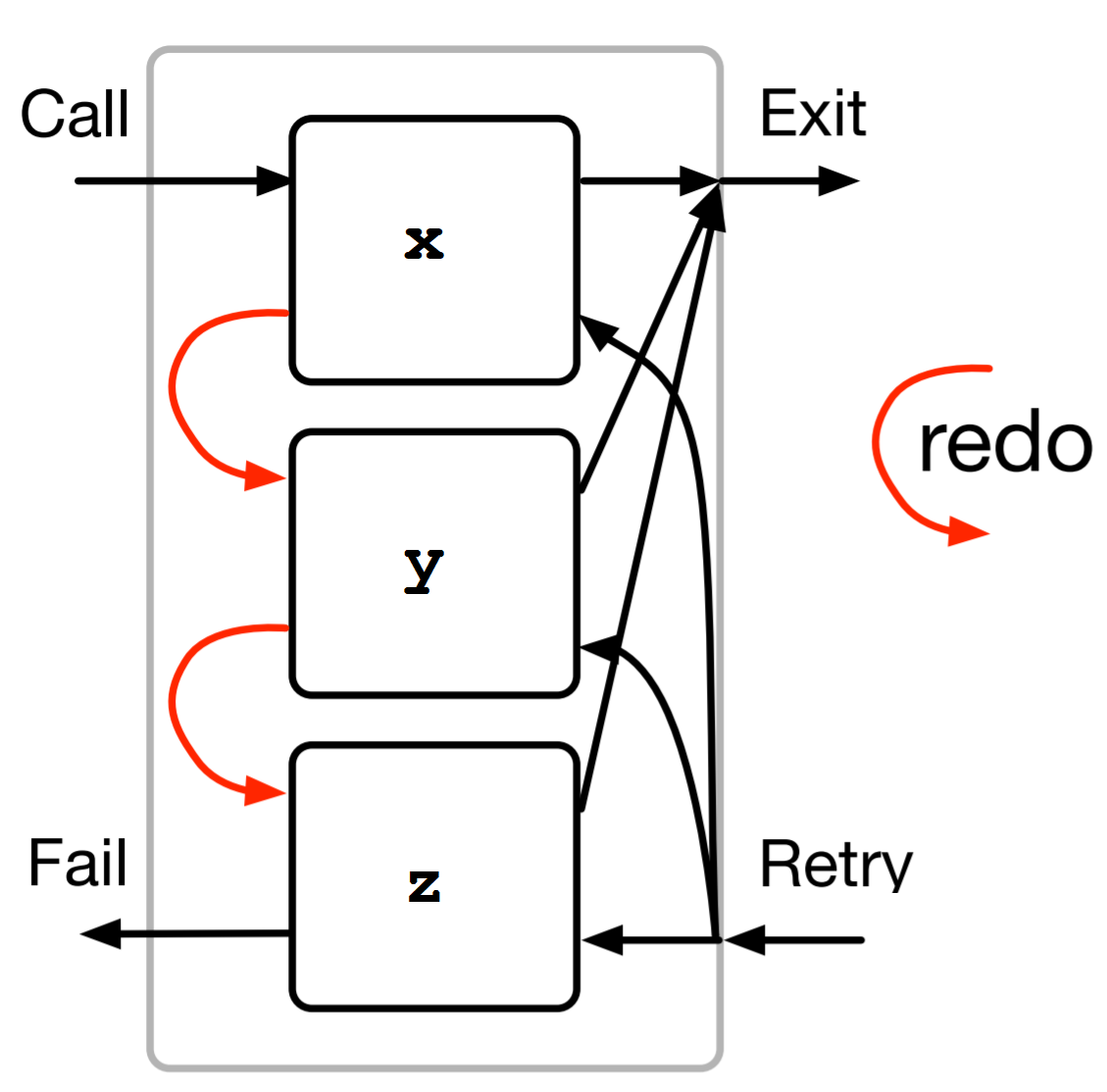
Prolog tries the clauses for a particular atom in order from top-to-bottom. So:
wsucceeds (exits) whenxsucceeds.- If
xfails, failing out ofxleads to calling intoy. This is a “redo” in SWI-Prolog’s tracing results. - Similarly, if
yfails, failing out ofyleads to calling intoz. - Failing out of our last body
zleads to failing out ofwitself.
What if we need to retry into w?
Prolog “remembers” which clause it exited last and retries into that clause. This is much like Java’s call stack “remembers” which line/expression to return to from a function call when it completes.
Let’s try some more complex box matching! We’ll convert this program to the box model:
:- dynamic blox/0. % No clauses for blox.
fox :- sox, box.
fox :- nox, brix.
sox :- brix, blox.
box :- nox.
clox :- blox.
nox.
brix :- tix, nox.
brix :- box.
tix :- box.(Two Exercises.)
2 From Propositional Logic to Datalog
Datalog is a language used to express queries over databases with strong links to SQL. (Learn more in CPSC 304 or CPSC 368!)
Datalog is our next step “up” toward Prolog.
2.1 What’s Wrong with Propositional Logic?
Let’s talk about some CPSC courses:
| Course | Year | Section | Days | Time | Room |
|---|---|---|---|---|---|
| CPSC 312 | 2021 | 101 | MWF | 12:00 | DMP 310 |
| CPSC 322 | 2021 | 101 | TR | 14:00 | SWNG 121 |
| CPSC 322 | 2021 | 101 | TR | 17:00 | SWNG 121 |
Can we represent this information? Sure:
cpsc_312_2021_101_MWF_1200_DMP310.
cpsc_322_2021_101_TR_1400_SWNG121.
cpsc_322_2021_101_TR_1700_SWNG121.But, each of these is its own indivisible atom. We cannot talk about the relationships between the individual elements inside of them, except by writing out many, many more additional atoms and rules!
How about this instead:
scheduled(cpsc312, 2021, 101, mwf, 12, dmp310).
scheduled(cpsc322, 2021, 101, tr, 14, swng121).
scheduled(cpsc322, 2021, 101, tr, 17, swng121).Now, we need a syntax (and semantics, and proof procedure) to let us reason about these individual parts.
2.2 Datalog Syntax
In Datalog:
- A variable starts with an upper-case letter or underscore
_. (_itself is a special anonymous variable much like in Haskell.) - A predicate symbol is a sequence of letters, digits, or underscores, starting with a lower-case letter
- A constant is one of:
- a predicate symbol
- a number (sequence of digits)
- any sequence of characters between single quotes
- A term is either a variable or a constant.
- An atom is either a predicate symbol alone (like in propositional Prolog) or a predicate symbol with a list of terms in parentheses, like:
p(t1, ..., tn).3
So, in Datalog, scheduled(cpsc322, 2021, 101, tr, 17, swng121). is a fact made up of a single atom with a list of six terms.
Spoiler: In full Prolog, we’ll let a term look, recursively, like that more complex form of atom. It can be a symbol with a list of terms inside parentheses, and those terms can also be symbols with lists of terms inside parentheses, etc.
(Exercise.)
Knowledge bases, queries, and definite clauses in Datalog are just like propositional definite clauses: facts and rules.
However, all the atoms (the one in a fact or the head of a rule, the ones in a rule body or query) can now be of the form p(t1, ..., tn).
How does that help us?
Consider our lighting domain:
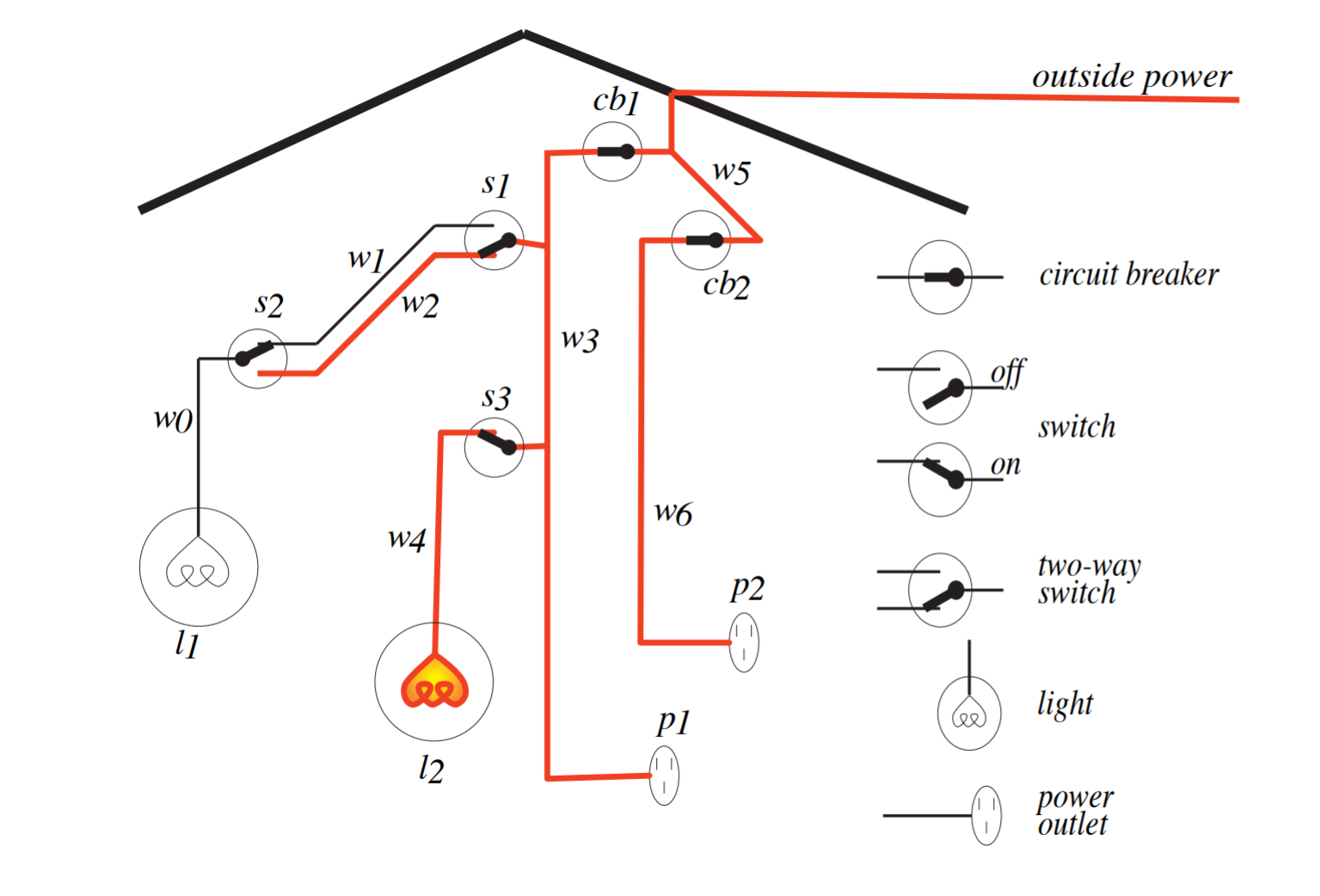
We used to have atoms like ok_l1, lit_l1, live_outside, and live_w3.
But there’s no relationship in Prolog between the l1 in ok_l1 and lit_l1! There’s no relationship between the live in live_outside and live_w3.
Now, we can separate out properties like liveness, being ok, and being lit from individuals like light #1, the outside wire, and wire 3: ok(l1), lit(l1), live(outside), live(w3).
That means instead of writing specific rules like:
live_l1 :- live_w0.
live_w0 :- live_w1, up_s2.
live_w0 :- live_w2, down_s2.We can write general rules like:
live(X) :- connected_to(X,Y), live(Y).which means X is live if X is connected to Y and Y is live.
2.3 Variables in Datalog
Variables are universally quantified in a Datalog rule, just like Haskell type variables were.
In Haskell, if map has the type (a -> b) -> [a] -> [b], it means that for any types a and b, map takes a function from a to b and a list of as and returns a list of bs.
In Prolog, live(X) :- connected_to(X, Y), live(Y). says for any values of X and Y, if connected_to(X, Y) and live(Y) are both true, then live(X) is true.
(How will Prolog figure out what “values” to match up with X and Y? Unification! We’ll come back to that.)
2.4 Practice with Datalog
Let’s practice describing our lighting domain with Datalog. Again, we’ll describe power outlet #2.
We’ll use some of the following individuals in our program:
pX,lX,wX,cbX,sX: with a number in place ofXlikep2orcb1, these are power outlet #X, light #X, wire #X, circuit breaker #X, and switch #X.outside: the outside power source
We’ll use some of the following relations:
power(X),light(X),wire(X),breaker(X),standard_switch(X): each identifies what type of thing an individual is;Xis, respectively: a power outlet, a light, a wire, a circuit breaker, or a standard switch.working(X): individualXis working (not broken), used for circuit breakers and lightsup(S):Sis in its “up” position, used for switchesok(X): individualXis capable of doing its job, defined separately for wires and power and the outside power source (automatically true), and for lights and circuit breakers (true only if they’re working), and for standard switches (true only if they’re in the up position)live(X): individualXis live; always true of the outside power; otherwise, true ifXis connected to something that is itself bothokandliveconnected_to(X, Y): individualXis connected to (can receive power from) individualY
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% General rules: this section is true
% regardless of the specific circuit diagram
% we are describing (as long as we have the
% given types of elements in it).
ok(outside).
ok(W) :- wire(W).
ok(P) :- power(P).
ok(CB) :- breaker(CB), working(CB).
live(outside).
live(X) :- connected_to(X, Y), ok(Y), live(Y).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% This is the description of this particular circuit:
power(p2).
breaker(cb2).
wire(w6).
wire(w5).
connected_to(p2, w6).
connected_to(w6, cb2).
connected_to(cb2, w5).
connected_to(w5, outside).
working(cb2).
% Aside: it may be useful to have things like:
%
% :- dynamic power/1.
%
% to say that power (which takes one term) is
% dynamic and may be defined later.
%
% That makes describing the individual circuits
% a bit easier, since you don't need to group
% all power(...) clauses together. It also means
% Prolog won't complain if you have no power(...)
% clauses.Now we can ask if power outlet p2 is live with the query: ?- live(p2).
(Two Exercises.)
2.5 Semantics of Datalog
There is a lot to say about the semantics of Datalog.
- What is an “individual”? They’re not just
trueorfalse. - How do we tell if an atom is
trueorfalse, when that may depend on its list of terms? - How do we deal with variables (besides just saying “unification”)?
- What does a proof look like?
However, we’re going to hold onto those questions until we define full Prolog.
3 Terminology Summary
Here’s some of this unit’s terminology: box model, call, exit, fail, retry, datalog, variable, predicate symbol, constant, term, atom (for Datalog, an expansion of atom for propositional logic),
You can stop tracing with
nodebug.↩︎For now, a particular atom can only succeed or fail. If it succeeds, retrying it won’t somehow make it “succeed differently”. Thus, our only retry option is to chain retries backward until we reach the start of attempting to call an atom with multiple clauses and move on to that atom’s next clause. However, later success will also come with a substitution imposed by unification. So, now we may be able to retry any goal and succeed with a different substitution, which may allow subsequent goals to succeed. You can see an example of an atom succeeding differently, but it requires either full Prolog or at least Datalog, not just propositional logic.↩︎
Don’t read this if you get easily confused by terminology. What we call an atom is sometimes called a compound term. In that case, what we call a predicate symbol is instead called an atom.↩︎

