Introduction to Prolog

1 Starting Prolog

Prolog is a logic programming language. Where Haskell focuses on functions, Prolog focuses on relations: ways to define properties that hold for some sets of objects in the world but do not hold for others.

There are some interesting relationships between Haskell and Prolog.

Pattern-matching:

• Haskell has powerful and concise pattern-matching facilities that are central to the language.
• Prolog has even more powerful pattern-matching facilities that are even more central to how the language works. (Using unification!)

Easy construction of tree-like data:

• Haskell makes it easy to create new algebraic data types.
• Prolog makes it easy to freely construct tree-structured data.

Static type checking (or not):

• Haskell has a powerful type system that shapes how programmers think in the language and gives tremendous (and sometimes overwhelming) feedback about the correctness and meaning of programs.
• Prolog.. doesn’t do a lot with types. It largely leaves monitoring correctness and structure of your data to you and to run-time.

Prolog began as a way to write and understand natural language systems and turns out to have powerful connections to database languages.

Let’s dive in. We’re going to work our way “up” from propositional logic to datalog to Prolog itself. Along the way, we’ll spend a lot of time on meaning and intent and how they connect to programs.

2 A Little Bit of Logic

Prolog stands for programming in logic. So, let’s begin with a bit of logic.

2.1 Propositional Logic

A proposition is a simple statement that is either true or false. Simple statements might be “the light is on” or “Eleanor is Steve’s daughter”, but they generally wouldn’t be more complex like “The light is on, and Naomi is Steve’s daughter.”

An atom represents a proposition and is a word that starts with a lower-case letter (and can contain letters, digits, and underscores). So, we might represent “the light is on” by light_on and “Steve plays ukulele” by sUkes. (Later, we’ll use something a bit richer to represent simple statements!)

We connect atoms together with conjuction (“and”), written as a comma. So, (light_on, sUkes) (or just light_on, sUkes) is true if both light_on and sUkes are true and false otherwise.

We’ll make logical statements as definite clauses. A definite clause is one of:

• an atomic clause or fact¹, which is just an atom followed by a period ., or
• a rule, which is of the form head :- body². The head is an atom. The body is any number of atoms joined by , (“anded” together), all followed by a period .

A fact essentially states that its atom is true. A rule states that the truth of its head follows from the truth of its body. (If the body is true, the head is as well. If the body is not true, then the rule says nothing about the head.)

A logic program or knowledge base is a set of definite clauses.³ It simply states that all of its clauses are true.

A query over that knowledge base is a body (a conjunction of atoms connected by ,). We can ask whether that query holds, based on the knowledge base.

Let’s practice a bit of the syntax of propositional definite clauses with an exercise!

(Exercise.)

2.2 An Example

Here’s an example. What’s wrong with it?

live_outside.
ok_cb2.
live_w5 :- live_outside.
live_w6 :- ok_cb2, live_w5.
p2 :- live_w6.

Seriously. Is this example OK? Is it a correct logic program? Why, or why not?

2.3 A Meaningful Example

Let’s describe a real-world domain with some logic. Here’s what the wiring for a house might look like:

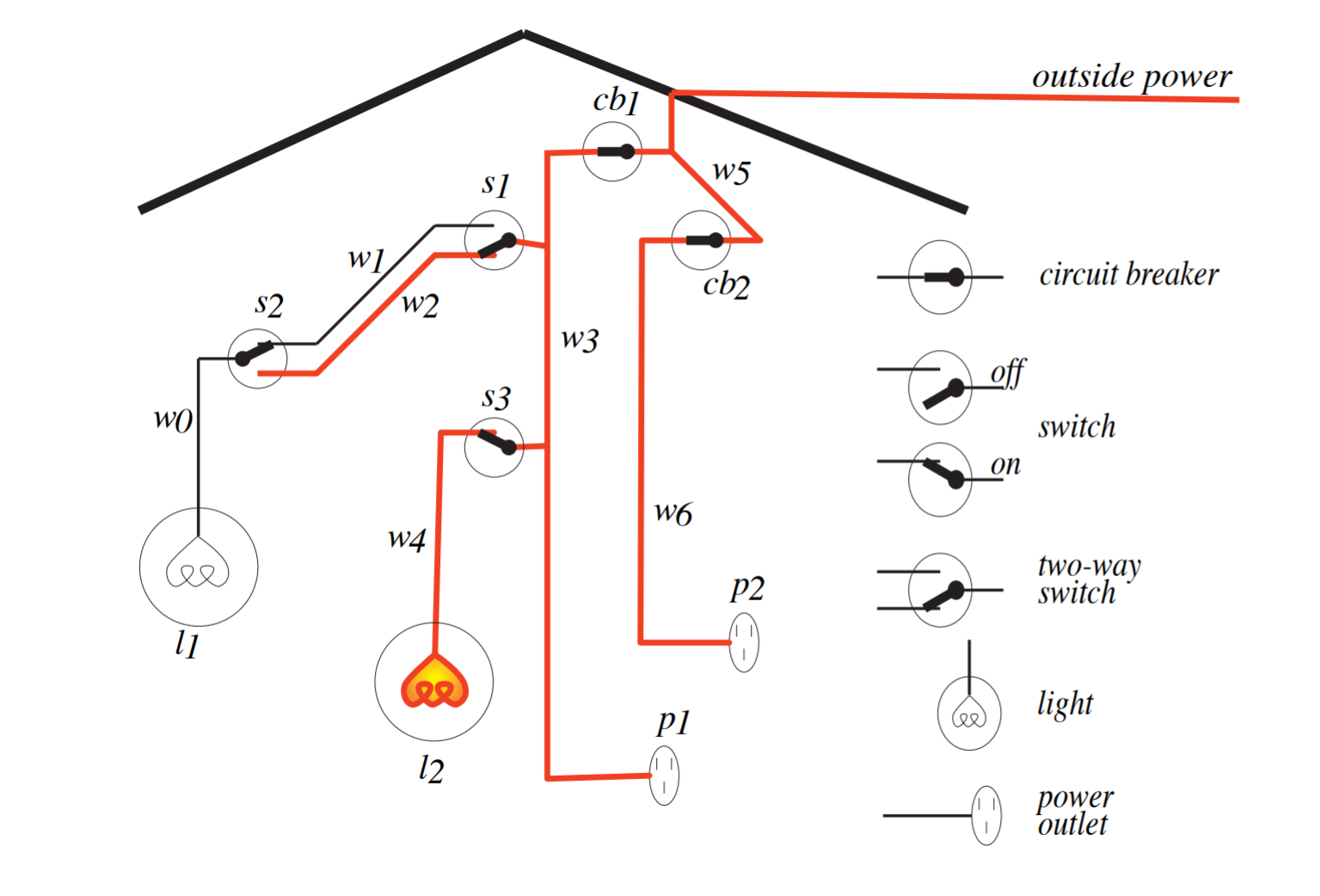
We’ll say that a wire is “live” if it has power supplied. A switch is either up or down. A circuit breaker is OK (letting power through) or not.

So, for example, we might describe the status of power outlet p2 using:

% Comments start with %
% The outside power is always live.
live_outside.

% Circuit breaker #2 is OK (working).
ok_cb2.

% Wire 5 is connected to the outside wire.
live_w5 :- live_outside.

% Wire 6 is connected to wire 5 if the circuit breaker is OK.
live_w6 :- ok_cb2, live_w5.

% Power outlet 2 is powered if wire 6 is live.
p2 :- live_w6.

Same example. Is it better now? (The comments are helpful, if a bit too detailed. But, even without them, do you see meaning now in the program?)

(Three Exercises.)

Let’s also play with this in SWI-Prolog (swipl)!

3 What Does a Program Mean?

In Haskell, we ignored I/O at first but eventually realized a program with no input or output is useless.

Similarly, a program’s result is only as useful as what it tells us about the world. But programs are not about the world; programs are just mechanical symbol manipulation!

When we write a program, we take ideas about the world and encode them in the programming language’s structures. Our understanding of the program’s intent gives it meaning in the world.

When we create a logic program, we’ll generally proceed in these steps to make it a meaningful program:

1. Understand the task domain: what is the world we want to describe and reason about in the computer?
2. Choose atoms in the computer to denote propositions (statements about the domain). These atoms have meaning to the knowledge base (KB) designer.
3. Tell the system knowledge about the domain (by creating a KB!).
4. Ask the system questions.

3.1 The User’s Perspective of Semantics

From the user’s perspective, with a “good” system:

1. The task domain is the intended interpretation of the program.
2. Each atom is associated with some proposition you want to represent.
3. Each clause is a statement that is true in intended interpretation. The clauses axiomatize the domain.
4. The system’s answer to the question is meaningful (and true!) in the intended interpretation based on the user’s associated meaning for the answer.

3.2 The Computer’s Perspective of Semantics

From the computer’s perspective:

1. It has no understanding of the intended interpretation.
2. Atoms are syntactic elements with no associated meaning.
3. The KB provides mechanical rules that relate the atoms.
4. A mechanical proof procedure lets the system reach conclusions from the KB.

3.3 In the Electrical Domain

In the user’s mind, each atom in the electrical domain means something in the world. Let’s describe that domain again in a somewhat different way:

• light1_broken: light 1 is broken
• sw1_up: switch 1 is up
  
• sw2_up: switch 2 is up
  
• power: there is power in the building
  
• unlit_light1: light 1 isn’t lit
  
• lit_light2: light 2 is lit

We can then axiomatize the world in the computer:

light1_broken :- sw1_up, sw2_up, power, unlit_light1.
sw1_up.
sw2_up
power :- lit_light2.
unlit_light1.
lit_light2.

These symbols and rules mean something to us, like “we know light 1 is broken if we observe that switches 1 and 2 are up, the building has power, but light 1 still isn’t lit.”

These symbols mean nothing to the computer. (Indeed, if we consistently rename any symbol to some new, unused one like foo, the program behaves exactly the same to the computer.)

However, it can mechanically derive from this KB: light1_broken.

We (the humans, trusting the system) can then conclude from this that light 1 is indeed broken.

3.4 Interpretations

To define the semantics of our programs and connect them to the intended semantics in the world, we’ll use some new terminology.

An interpretation I is one way to assign values to the pieces of our program. I:

• assigns a truth value to each atom

• yields a truth value for each compound proposition based on their truth tables:

  p	q	p, q	p :- q
  true	true	true	true
  true	false	false	true
  false	true	false	false
  false	false	false	true

• So:

  • a body p, q is true in I if both p and q are true in I (and the body is false otherwise)
  • a rule h :- b1, b2, ..., bk is false in I if all its body atoms b1, b2, …, bk are true but h is false (and the rule is true otherwise)
  • a KB is true in I if every clause in the KB is true in I (and the KB is false otherwise)

3.5 Models and Logical Consequences

Some interpretations don’t make sense for our program.

• A model of a KB is an interpretation in which every clause in the KB is true.
• A particular conjunction of atoms (a “body”) g is a logical consequence of a KB if g is true in every model of the KB.⁴ We write that: KB ⊨ g

Intuitively, a logical consequence of a program is anything that’s true in every sensible interpretation of that program.

(Three Exercises)

3.6 Proofs and Entailment

It would be nice if Prolog discovered logical consequences for us!

We want a proof procedure: a mechanical method to derive a demonstration that a formula logically follows from a KB.

We’ll say KB ⊢ g means there is a proof that g can be derived from knowledge base KB.

We don’t just want any proof procedure. We want a good one:

• It doesn’t lie: A proof procedure is sound if KB ⊢ g implies KB ⊨ g.
• It doesn’t miss things: A proof procedure is complete if KB ⊨ g implies KB ⊢ g.

4 A Proof Procedure: Top-Down Resolution

The proof procedure we will focus on is top-down (SLD) resolution⁵. We will start with a goal to prove (the g in KB ⊢ g) and work our way backward looking for rules and facts that establish the goal.

For this part, we’ll think of facts h. as being h :- . That is, a fact is like a rule with nothing in its body.

4.1 A Top-Down Proof

A proof (or derivation) of a query ?- g1, g2, ..., gi:

• Starts with an answer clause of the form yes :- g1, g2, ..., gi.

• Aims to prove yes by repeatedly modifying and elaborating the clause until it is the simple fact: yes :- .

• At each step performs resolution of the answer clause with a KB clause g1 :- b1, b2, ..., bn..

  The result is the new answer clause:

  yes :- b1, b2, ..., bn, g2, ..., gi.

  That is: it has as its goals the body of our rule plus all except the first goal in our answer clause.⁶

Let’s try that out!

Here is a KB:

live_outside.
ok_cb2.
live_w5 :- live_outside.
live_w6 :- ok_cb2, live_w5.
p2 :- live_w6.

Let’s prove the query ?- p2:

yes :- p2.
% Continue from here!

Notice that we always work from the previous line and some clause in the KB. We start with our query in the body of our answer clause and end with nothing in the body of the answer clause.

(Three Exercises.)

4.2 Prolog’s Proof Procedure

Prolog tries to build a top-down derivation starting from our query. It needs to decide two things:

1. Which goal in the answer clause should we try next?

   Prolog always tries the first. Logically, it doesn’t matter. They all need to be true to establish the answer.⁷

2. Which clause (rule/fact) should we use next?

   Prolog always tries them in order from top to bottom.

Unfortunately, some choices of clause to use may lead to successful derivations and some may not!

If Prolog runs into a failed derivation, it backtracks until it finds a different clause to try and starts again to develop its proof.

4.3 Visualizing the Proof Procedure

We can see what Prolog’s proof procedure looks like as a diagram. Imagine we ask the query ?- a, d from the KB:

% Each atom's rules are on one line to keep it short!
:- dynamic j/0, m/0, c/0. % needed to avoid errors
a :- b, c.     a :- g.     a :- h.
b :- j.        b :- k.
d :- m.        d :- p.
f :- m.        f :- p.
g :- m.        g :- f.
h :- m.
k :- m.
p.

Prolog will explore the proof in this order:

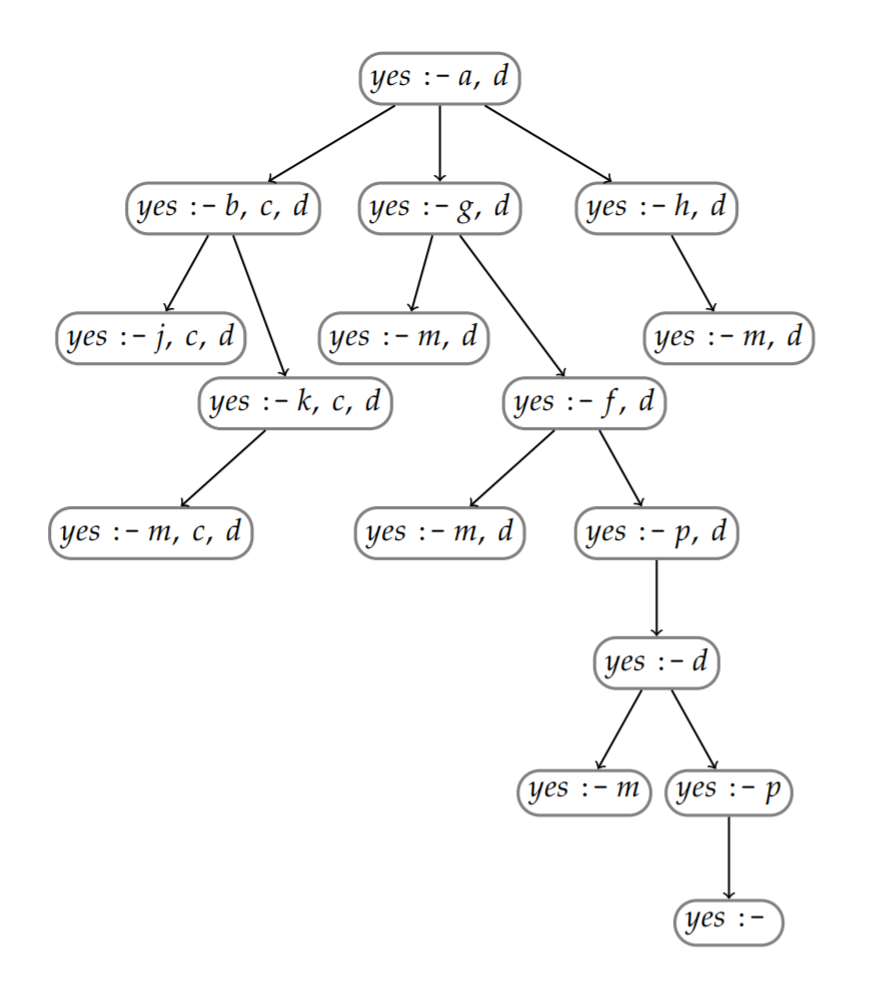
(Prolog only gets to the rightmost branch of the tree that starts yes :- h, d if we hit ; to ask for more results.)

We call this top-down, depth-first search. You can learn much more about that in CPSC 322!

4.4 How Good is Prolog’s Proof Procedure?

Is Prolog’s proof procedure sound?

Well, Prolog traces through a complete derivation any time it comes back with the answer yes. What do we know from that derivation?

Is Prolog’s proof procedure complete?

Consider this KB. What will Prolog do with it and the query ?- a?

a :- a.
a :- b.
b.

(Two Exercises.)

5 Terminology Summary

A great bonus point activity would be to post and curate a summary of our terminology, like: atom (for propositional logic), conjunction, body, head, rule, clause or definite clause (for propositional logic), knowledge base/KB, interpretation, model, logical consequence, proof and proof procedure, derivation, ⊨ (“entailment” or “semantic entailment”) and ⊢ (proves/establishes or “syntactic entailment”), answer clause, resolution, soundness and completeness (of a proof procedure, and especially of Prolog!). Did we miss any? Probably :)