A Brief Introduction to Definite Clause Grammars and Difference Lists

1 Grammars in Prolog, Part 1

Prolog was originally created for natural language applications. What makes it suitable for that?

1.1 “Context-Free” Grammars

A common tool for describing languages (both natural and computing) is a “context-free grammar” or CFG. A CFG looks like a series of rules, each of which has the name of some portion of the grammar on the left and one way to break that portion of the grammar down on the right.

For example:

• We can describe a sentence like “a student likes the course” as a noun phrase (“a student”) followed by a verb phrase (“likes the course”).
• The noun phrase “a student” breaks down into its determiner (like “a”, “an”, or “the”) and its noun. In this case, that’s “a” and “student”.
• The verb phrase breaks down into the verb “likes” and another noun phrase: “the course”.

We can describe these rules in a CFG:¹

sentence = noun_phrase, verb_phrase ;
noun_phrase = determiner, noun ;
verb_phrase = verb, noun_phrase ;
determiner = "a" ; determiner = "the" ;
noun = "student" ; noun = "course" ; noun = "teacher" ; noun = "puppy" ;
verb = "likes" ; verb = "teaches" ; verb = "studies" ; verb = "tackles" ;

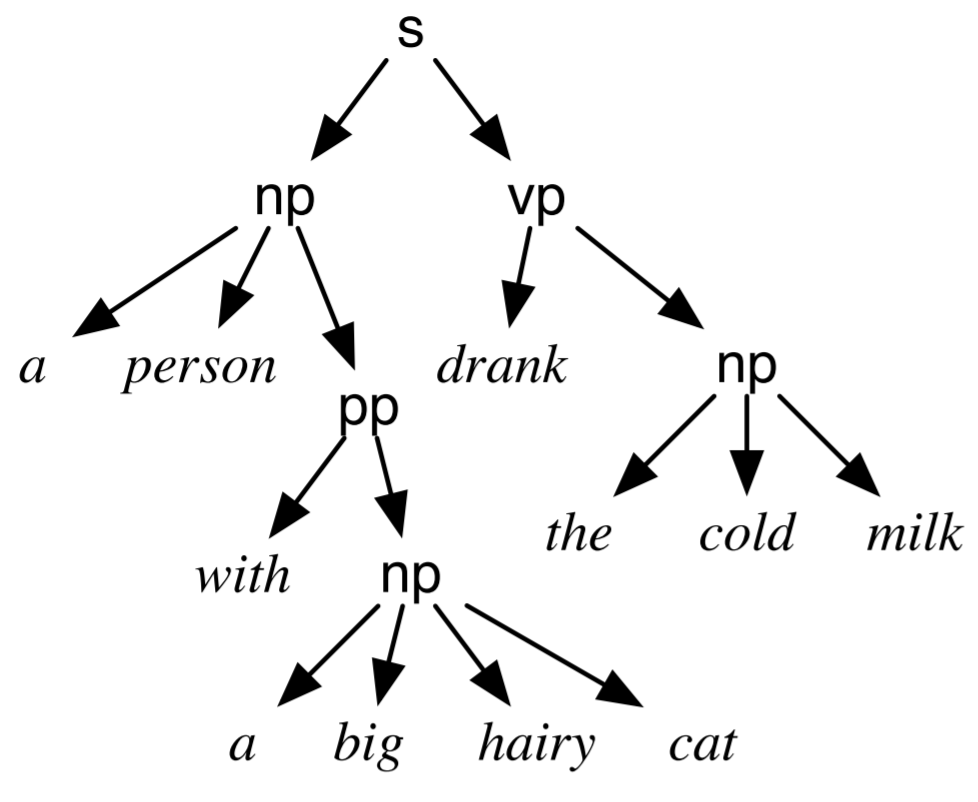
Using rules like this, we can determine if a sentence is “grammatical”, and we can “parse” a sentence to discover some of its structure. For example, here’s a possible “parse tree” from a slightly more complex grammar for the sentence: a person with a big hairy cat drank the cold milk:

1.2 Prolog is for Lovers, of Grammars

That grammar structure works surprisingly well in Prolog! Let’s make a Prolog program that parses sentences represented as lists of constants (symbols). To fit it on the screen, we’re using short names!

s(Words) :- np(NPWords), vp(VPWords), append(NPWords, VPWords, Words).
np(Words) :- det(DetWords), noun(NounWords), append(DetWords, NounWords, Words).
vp(Words) :- verb(VerbWords), np(NPWords), append(VerbWords, NPWords, Words).

det([a]). det([the]).
noun([student]). noun([course]). noun([teacher]). noun([puppy]).
verb([likes]). verb([teaches]). verb([studies]). verb([tackles]).

Here is a file with that grammar.

Now, we can run a query like ?- s([a, student, likes, the course]). and Prolog confirms it’s grammatical. We could add more arguments in order to extract more information (like the actual parse tree) if we wanted to.

This is Prolog, however, so we get neat stuff like every sentence about the puppy for free: ?- Sentence = [the, puppy|_], s(Sentence).

Cool!

But, let’s make things a little more complex.

2 Grammars in Prolog, Part 2

The student likes the puppy and the teacher likes the puppy. Right?

We can extend our grammar to handle compound sentences. There are some subtleties to the Prolog we choose here, but we’ll ignore them:

s(Words) :- simple_s(Words).
s(Words) :- simple_s(FirstWords), conj(ConjWords), s(RestWords), append(FirstWords, SecondWords, Words), append(ConjWords, RestWords, SecondWords).
simple_s(Words) :- np(NPWords), vp(VPWords), append(NPWords, VPWords, Words).
np(Words) :- det(DetWords), noun(NounWords), append(DetWords, NounWords, Words).
vp(Words) :- verb(VerbWords), np(NPWords), append(VerbWords, NPWords, Words).

conj([and]).
det([a]). det([the]).
noun([student]). noun([course]). noun([teacher]). noun([puppy]).
verb([likes]). verb([teaches]). verb([studies]). verb([tackles]).

Here is a file with our extended grammar.

2.1 Problems in our Grammar

Let’s try parsing our sentence now: ?- s([the, student, likes, the, puppy, and, the, teacher, likes, the, puppy]).

What happens?

Worse yet, let’s try parsing something that isn’t grammatical: ?- s([the, puppy, teacher, the]).

What happens?

OK, but that really only happens because we put the appends at the end. We’re not tying our rules to the actual input words early on. We can switch that around:

s(Words) :- simple_s(Words).
s(Words) :- append(FirstWords, SecondWords, Words), append(ConjWords, RestWords, SecondWords), simple_s(FirstWords), conj(ConjWords), s(RestWords).
simple_s(Words) :- append(NPWords, VPWords, Words), np(NPWords), vp(VPWords).
np(Words) :- append(DetWords, NounWords, Words), det(DetWords), noun(NounWords).
vp(Words) :- append(VerbWords, NPWords, Words), verb(VerbWords), np(NPWords).

conj([and]).
det([a]). det([the]).
noun([student]). noun([course]). noun([teacher]). noun([puppy]).
verb([likes]). verb([teaches]). verb([studies]). verb([tackles]).

Here is a file with our grammar with appends at the start.

That’s better, and it handles both of the cases above. However, notice what it’s doing now: It’s trying every single way to split the input each time it does an append and then checking if it split correctly. That’s both inefficient because we’re not paying attention to the grammar rules as we go and because of all the intermediate lists we’re building.

2.2 Interlude

Quick interlude. What is the result of: ?- append([1, 2, 3], Waiting, Result).

Result = % fill in the blank!

That’s neat. It’s a list whose end is still-to-be-determined: [1, 2, 3 | Waiting].

3 Grammars in Prolog, Part 3

Our solution so far takes the list of words and tries to “guess” the right split of the words and then check to see if that split is correct. It also does a bunch of inefficient appending.

We really want to say something like: “There’s a noun phrase at the start of this input list A, and the remaining input left over is this resulting list B.”

So, let’s say that.

Let’s start with just noun phrases:

np(InitialWords, RemainingWords) :- det(DInit, DRem), noun(NInit, NRem).  % Not quite.

Huh. We now need initial words and remaining words for determiner and noun as well. How do we stitch that together to make a noun phrase?

Well:

• The determiner comes at the start of the noun phrase. So, its initial words are the same as the noun phrase’s initial words.
• The noun comes next. So, its remaining words are the same as the noun’s initial words.
• The noun also comes last in the noun phrase. So, it’s remaining words are the same as the noun phrase’s remaining words.

All together, then:

np(InitialWords, RemainingWords) :- det(InitialWords, DRestWords), noun(DRestWords, RemainingWords).

What about, say, determiner. It’s just one word (or one of two options, anyway). What does it look like?

Well, the initial words must start with that one word:

det([a|Rest], Rest).
det([the|Rest], Rest).

OK! Now we’re ready to switch over the whole grammar:

s(IWords, RWords) :- simple_s(IWords, RWords).
s(IWords, RWords) :- simple_s(IWords, SSRWords), conj(SSRWords, CRWords), s(CRWords, RWords).
simple_sentence(IWords, RWords) :- np(IWords, NPRWords), vp(NPRWords, RWords).
np(IWords, RWords) :- det(IWords, DRWords), noun(DRWords, RWords).
vp(IWords, RWords) :- verb(IWords, VRWords), np(VRWords, RWords).

conj([and|Rest], Rest).
det([a|Rest], Rest). det([the|Rest], Rest).
noun([student|Rest], Rest). noun([course|Rest], Rest). noun([teacher|Rest], Rest). noun([puppy|Rest], Rest).
verb([likes|Rest], Rest). verb([teaches|Rest], Rest). verb([studies|Rest], Rest). verb([tackles|Rest], Rest).

Here is a file with our amazing difference-list grammar!

Where did all the appending go?

Answer: it’s gone! We do still work our way through the list (by unification against our bottom four predicates’ facts). However, we never do any unnecessary splitting/appending!

We may also want an entry point (sentence or s for us) to our grammar that doesn’t use difference lists. We can get there by ensuring that the “remaining words” from the input after parsing are empty so that the whole input list is the sentence:

s(Words) :- s(Words, []).  

Let’s do some exercises:

• translating an EBNF-style grammar into a Prolog implementation with difference lists
• writing other code that uses difference lists for efficient list manipulation

(Three Exercises. (One is still coming soon!))

Our still-to-be-written exercise is:

Reminder:

% A BST will be one of:
% + empty
% + node(Key, Value, LeftSubtree, RightSubtree), where 
%     all keys in LeftSubtree are less than Key, and
%     all keys in RightSubtree are greater than Key.

A “range query” in a BST collects all the values in the BST between two specified keys. In this problem, you’ll implement a predicate range_query(Tree, KeyLo, KeyHi, ValuesInit, ValuesRest) that is true when ValuesRest is a tail of ValuesInit (i.e., they are a difference list), and the portion of ValuesInit before ValuesRest is a list of all the values in Tree whose keys are greater than or equal to KeyLo and less than or equal to KeyHi. You may assume that Tree, KeyLo, and KeyHi are all ground and that Tree is a valid binary search tree.

4 So Much More!

There’s much much more to learn about DCGs plus Prolog-and-AI than what we’ve reached!

For a little taste, try David Poole’s little natural language question-answering system from CPSC 312 last year. (David didn’t use DCG syntax but used the methods we discussed plus some new ones!)