Negation as Failure

Lecture #12
Complete the associated in-class exercises.

Table of Contents

1 Why Bother with Negation?

This may seem obvious but… why should we bother defining negation? Do we need it?

Imagine we have a Prolog program that defines enrolled(Student, Course), which is true when student Student is enrolled in course Course. We’d like to use this to define empty(Course) that is true when Course has no students enrolled.

Can we define it?

What if we had some magical Prolog operator that somehow means negation. Let’s give it the strange name \+ so it won’t be confused with “logical negation”.

Now can we define empty(Course)?

 

Sure: empty(Course) :- \+ enrolled(Student, Course).

But what does that actually mean in Prolog?

 

2 Negation as Failure

Prolog will define negation of a goal as a failure to prove the goal is true. Why, and what does that mean?

 

2.1 A Reminder of Semantics

First, recall what it means to us for Prolog to prove a goal. When Prolog proves goal g follows from knowledge base KB, we rely on Prolog’s soundness to conclude that g is a logical consequence of KB: KB ⊨ g.

That means that g is true in every model of KB.

Consider this little knowledge base, which we’ll call KB1:

good(Course) :- favorite_topic(Topic), about(Course, Topic).

favorite_topic(prolog).
about(cpsc312, prolog).
about(cpsc313, systems).

Let’s ask some questions about this KB:

(Exercise.)

 

2.2 All Models, Some Models, or No Models?

We know that KB1⊨ good(cpsc312). We can read that as: “The truth of good(cpsc312) follows from the truth of the knowledge base.”

What does it mean that KB1⊭ good(cpsc313)?

Literally, it means: “It is not the case that the truth of good(cpsc313) follows from the truth of the knowledge base.”

So, does it follow from the knowledge base that good(cpsc313) is false?

(Exercise.)

 

good(cpsc312) is true in all models of our KB, and good(cpsc313) is true in some models of our KB and false in others.

(Exercise.)

 

The definite clause language we have learned up to this point is monotonic: adding clauses cannot invalidate a previous conclusion. That means there is nothing at all we can write (besides arithmetic) that is false in all models of our KB. Our knowledge base is always open to some new piece of information (some new fact or rule).

Unfortunately, that also makes it awkward to talk about negation. We cannot choose “the negation of a goal is true” to mean “the goal is false in all models of our KB”, because no goal is false in all models of our KB!

 

2.3 Assumptions Behind Negation as Failure

Instead, if we want to use negation in Prolog, we will make a very strong assumption: the Closed World Assumption.

We assume that our knowledge base describes everything that is true about the world. Anything that does not follow from our knowledge base is false.

This is negation-as-failure: Anything that we conclusively fail to prove is false. This assumption is why swipl says false when it fails to prove a goal, but we prefer to say no (meaning “no, I cannot prove it” rather than “false, it is not true”).

We’re explicitly saying here that our knowledge base is not open to any new facts or rules. The world is “closed” to new information being added.

 

2.4 Unique Names Assumption

There’s one perhaps-surprising consequence of our closed world assumption: We have also assumed that two different ground terms (e.g., constants or compound terms without variables) refer to different individuals in our domain. Names are unique.

Remember our knowledge base above:

good(Course) :- favorite_topic(Topic), about(Course, Topic).
favorite_topic(prolog).
about(cpsc312, prolog).
about(cpsc313, systems).

Under the closed world assumption, we can prove both good(cpsc312) and \+ good(cpsc313). (Sorry, CPSC 313, this is clearly not true in the real world!)

That also means that cpsc312 and cpsc313 must not refer to the same individual in the domain.

 

2.5 A Mechanism for Negation-as-Failure

For a goal g, \+ g indicates that Prolog should attempt to prove g and:

  1. If it succeeds, fail the goal \+ g. (As usual, backtracking on this failure rolls back any substitution created.)
  2. If it fails (at which point it would already have rolled back any substitution created), succeed in the goal \+ g.

Note that we interpret “failure to prove” as “negation”. Note also that any substitution that may have been explored in trying to prove g is lost, no matter what.

 

We can understand negation-as-failure procedurally via the box model. For any goal a, \+ a is true when Prolog’s attempt to prove a fails:

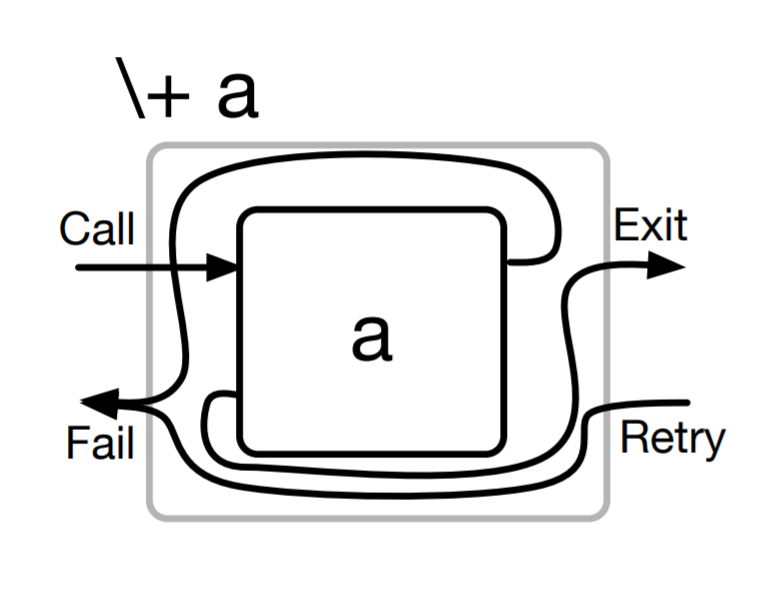
The positive goal’s call port is wired to the negated goal’s call port. Its exit port is wired to the negated failure, its failure to negated exit, and negated retry to its failure.

When we call into \+ a, we immediately call into a. Then:

 

3 Negation-as-Failure (\+) in Practice in Prolog

Let’s try out \+ in a Prolog program!

3.1 Removing an Element from a List

We want remove_all(Elt, InitList, RemList) to be true when RemList is InitList with all occurrences of Elt removed. Here’s a possible implementation:

remove_all(_, [], []).
remove_all(Elt, [Elt|IL], RL) :- remove_all(Elt, IL, RL).
remove_all(Elt, [ILStart|IL], [ILStart|RL]) :- remove_all(Elt, IL, RL).

Try this implementation out on some examples. What is wrong with it?

(Exercise.)

 

Unfortunately, that implementation of remove_all/3 succeeds on a query like remove_all(vanish, [vanish], [vanish]). Re-implement it using \+.

Hint: It is not necessary, but if we rewrite the second case as:

remove_all(Elt, [ILStart|IL], RL) :- Elt = ILStart, remove_all(Elt, IL, RL).

its head and recursive goal both look a little more like the third case’s. The second case requires that Elt and ILStart unify. What does the third case really require?

(Two Exercises.)

 

3.2 What Can Go Wrong with Negation-as-Failure

Our implementation of remove_all(Elt, InitList, RemList) that used \+ Elt = ILStart as a goal worked perfectly when Elt and InitList were ground, but incorrectly fails on a simple query like remove_all(Result, [1, 2], [1]). What goes wrong?

Here’s our implementation:

remove_all(_, [], []).
remove_all(Elt, [Elt|IL], RL) :- remove_all(Elt, IL, RL).
remove_all(Elt, [ILStart|IL], [ILStart|RL]) :- 
   \+ Elt = ILStart, remove_all(Elt, IL, RL).

Let’s take it step-by-step:

  1. Prolog tries to prove remove_all(Result, [1,2], [1]).
  2. That does not unify with the first clause remove_all(_, [], [])., which makes sense.
  3. That does unify with the head of the second clause remove_all(Elt1, [Elt1|IL1], RL1), with Result = 1, Elt1 = 1, IL1 = [2], and RL1 = [1]. We humans can look aheand and see this choice won’t work because the wrong element was removed from [1, 2], but Prolog needs to do a bit of searching before it figures that out:
    1. Prolog tries to prove the new goal remove_all(1, [2], [1]).
    2. That doesn’t unify with the first clause, which makes sense.
    3. That doesn’t unify with the head of the second clause (because 1 is not the first element of [2]), which makes sense.
    4. That doesn’t unify with the head of the third clause (because the first element of [2] is not the same as the first element of [1]), which makes sense.
  4. Prolog backtracks. The original goal remove_all(Result, [1,2], [1]) does unify with the head of third clause remove_all(Elt2, [ILStart2|IL2], [ILStart2|RL2]), with Elt2 = Result, ILStart2 = 1, IL2 = [2], RL2 = []. Now, Prolog has two goals to establish: \+ Result = 1, remove_all(Result, [2], []). That actually looks pretty good. We still haven’t chosen Result, the element to remove. Our recursive call will be on the list [2] and remaining list [], which we can make work by choosing to remove 2. BUT: Prolog proceeds left-to-right. So:
    1. Prolog tries to prove the new goal \+ Result = 1.
    2. To do that, Prolog tries to prove the goal Result = 1.
    3. Prolog easily succeeds in proving Result = 1 just by using the substitution Result = 1.
    4. That means Prolog didn’t fail to prove Result = 1, so the goal \+ Result = 1 fails.
  5. Prolog backtracks, but there are no more options to try. So it fails.

 

Do you see what happened? When we said \+ Result = 1, we intended something like the mathematical notion Result ≠ 1. However, that’s not how Prolog’s negation-as-failure works.

(Four Exercises. We’ll skip these in class. They’re a chance for you to explore some surprising and not-so-surprising negations. Read the feedback on the questions!)

 

Still, \+ is incredibly useful as long as we’re careful to use it where “Prolog cannot prove goal” really means what we intend when we say “goal is not true”. Try it out!

(Three Exercises. We’ll skip these in class.)

 

4 Implementing Negation and the Cut

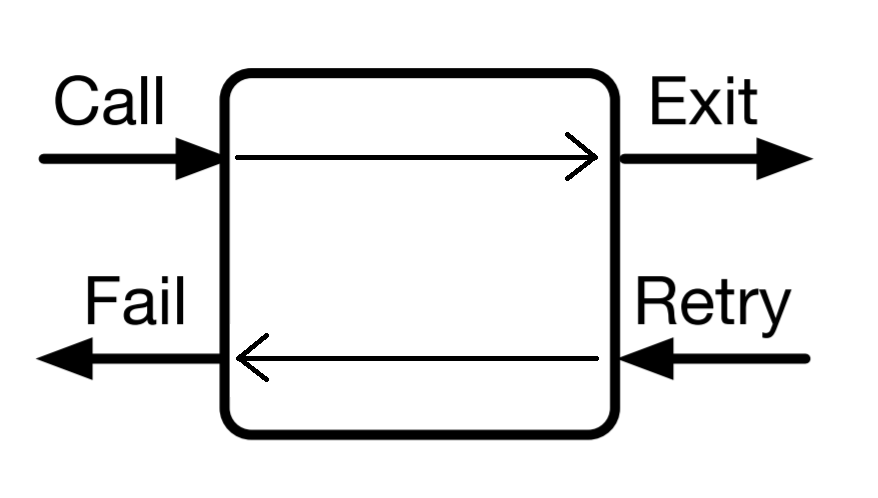
Let’s briefly discuss one last extra-logical predicate in Prolog: the cut written !.

! always succeeds. Where it becomes interesting is when it is retried: the retry port on ! is connected to its enclosing predicate’s fail port.

So, on the inside, a cut looks just like a fact:

Box model of cut on the inside looks just like a fact.

When a cut appears somewhere inside the definition of a predicate, its call, exit, and retry ports connect to its neighbors just like they should. However, its fail port skips all the previous goals in the current body and all the other clauses defining the predicate to fail out of the entire predicate:

Box model of cut inside a larger predicate fails the whole predicate.

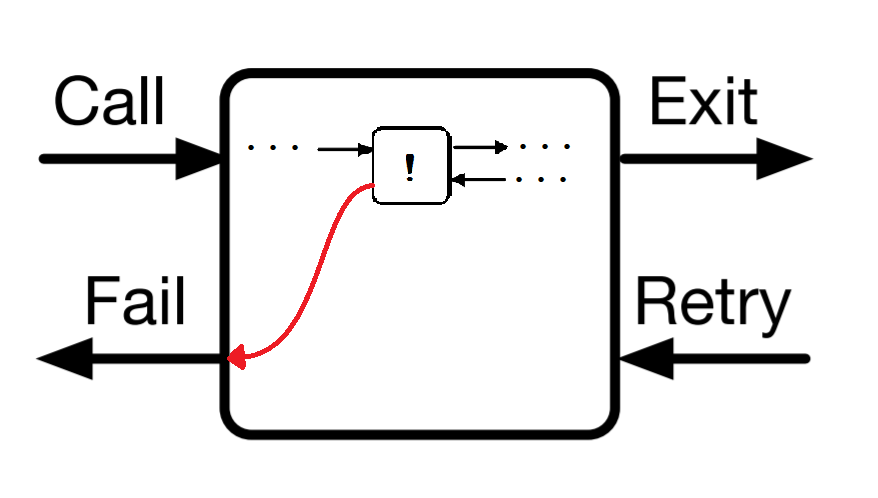
In other words, if we encounter ! as a goal while trying to prove some predicate, it has no special effect. But, if we try to backtrack across the cut, we ignore all the previous goals in that body and all the other clauses for that predicate and fail the predicate immediately.

 

We can implement negation-as-failure using the cut as long as Prolog also lets us take a term and “promote” it to be an atom (specifically, a goal):

% negation_as_failure(Goal) requires Goal to be a term that we can
% use like a normal goal. (It doesn't need to be ground, but it cannot
% be a variable!)
%
% negation_as_failure(Goal) fails if Goal is provable and suceeds if
% Goal is not provable:
negation_as_failure(G) :- G, !, fail.
negation_as_failure(G).

When Prolog tries to prove negation_as_failure(G), it begins with the first clause. That causes Prolog to first try to prove G. If that succeeds, it reaches the cut, which means it will never try the second clause. Then, it forces failure with fail/0. Since the second clause is no longer an option, negation_as_failure(G) fails overall.

If proving G fails in the first clause, then Prolog never reaches the cut. It then instead tries the second clause, which is a fact that automatically succeeds.

 

The cut is tremendously powerful but dangerous. It enables us to define new control constructs (like negation-as-failure), to “prune out” redundant solutions, and to avoid inefficient computations. However, you should use it very cautiously (and never in our quizzes unless explicitly asked) as, like negation, it can have surprising consequences!

Sadly, that’s all we have time for this term with the cut!

 

5 A Tiny Bit of Something diffferent

A \= B is the same as \+ A = B, meaning Prolog cannot prove that A and B unify.

This fails right away if A and B are different, free variables. That’s because in that case Prolog can unify them simply by setting them equal.

dif(A,B) solves this problem using some interesting new control structures in Prolog that enable constraint logic programming. It delays the constraint that A not unify with B until A and B are instantiated enough that we can tell whether they’re the same. You can use dif by adding :- use_module(library(dif)). to the top of your program.

Also sadly, that’s all we have time for this term on dif. Do try replacing \+ Elt = ILStart in remove_all with dif(Elt, ILStart) and see how it changes the functionality of that predicate!